Задания

Содержание

6.6. Задания#

6.6.1. Нули полинома Лежандра#

Методом Риддерса найдите нули полинома Лежандра \(L_7\). (Которые служат узлами квадратуры Гаусса.)

\[L_7(x) = \frac{1}{16}(429 x^7 - 693 x^5 + 315 x^3 - 35 x).\]

6.6.2. Вычисление квадратного корня#

Напишите функцию mysqrt(x), вычисляющую квадратный корень \(\sqrt{x}\) для неотрицательного \(x \ge 0\). Сравните невязку написанной вами функции со стандартной функцией sqrt(x) в диапазоне range(0, 10; step=0.1).

6.6.3. Уравнение фазовых концентраций#

Уравнение фазовых концентраций (Rachford-Rice equation) используется для расчётов парожидкостного равновесия смеси веществ [02]. Уравнение выводится из массового баланса веществ в каждой фазе и представляет собой

\[ F(G) = \sum_{i} \frac{z_i \times (K_i - 1)}{G \times (K_i - 1) + 1} = 0, \]

где \(z_i\) мольная доля \(i\)-го компонента в смеси, \(K_i\) константа равновесия \(i\)-го компонента (отношение мольной доли компонента в газе к его мольной доли в жидкости) и \(G\) мольная доля газа в двухфазном состоянии.

Решение этого уравнения показывает мольную долю газа в двухфазном состоянии при соответствующем распределении компонентов по жидкой и газовой фазе.

Можно показать [02], что решение уравнения стоит искать в интервале

\[ 1 / (1 - \max K_i) \quad \ldots \quad 1 / (1 - \min K_i). \]

Этот интервал содержит в себе физические значения мольной доли газа \(G\), а функция \(F(G)\) на нём убывает.

Задание

Напишите функцию rachford_rice_solve(z, K) -> G, решающую уравнение фазовых концентраций. Постройте график функции \(F(G)\) и найденный корень уравнения \(F(G) = 0\) для случаев

\(z = [0.9, 0.1]\), \(K = [1.5, 0.01]\);
\(z = [0.2463, 0.2208, 0.2208, 0.3121]\), \(K = [40, 25, 0.6, 0.005]\).

Для построения графиков воспользуйтесь пакетом Plots.jl.

6.6.4. Бинодаль уравнения состояния ван дер Ваальса#

Примечание

В этом задании вам предстоит найти область двухфазного равновесия для уравнения состояния ван дер Ваальса.

В приведённых величинах \(P_r = P / P_c\), \(V_r = V / V_c\), \(T_r = T / T_c\) уравнение ван дер Ваальса имеет вид

\[P_r(V_r, T_r) = \frac{8 T_r}{3 V_r - 1} - \frac{3}{V_r^2}.\]

Несложно построить набор изотерм.

pressure(Vr::Real, Tr::Real) = 8Tr / (3Vr - 1) - 3 / Vr^2
V = range(0.34, 5; length=200)
plt = plot(;
    ylim=(0, 2),
    xlim=(0, 5),
    xlabel=L"V/V_c",
    ylabel=L"P/P_c",
    lw=2,
)
for Tr in (0.85, 0.9, 0.95, 1.0, 1.1)
    plot!(V, pressure.(V, Tr); label=L"T_r = %$(Tr)")
end
plt

Рассмотрим подробнее изотерму для докритической температуры \(T^* \in (0, T_c)\).

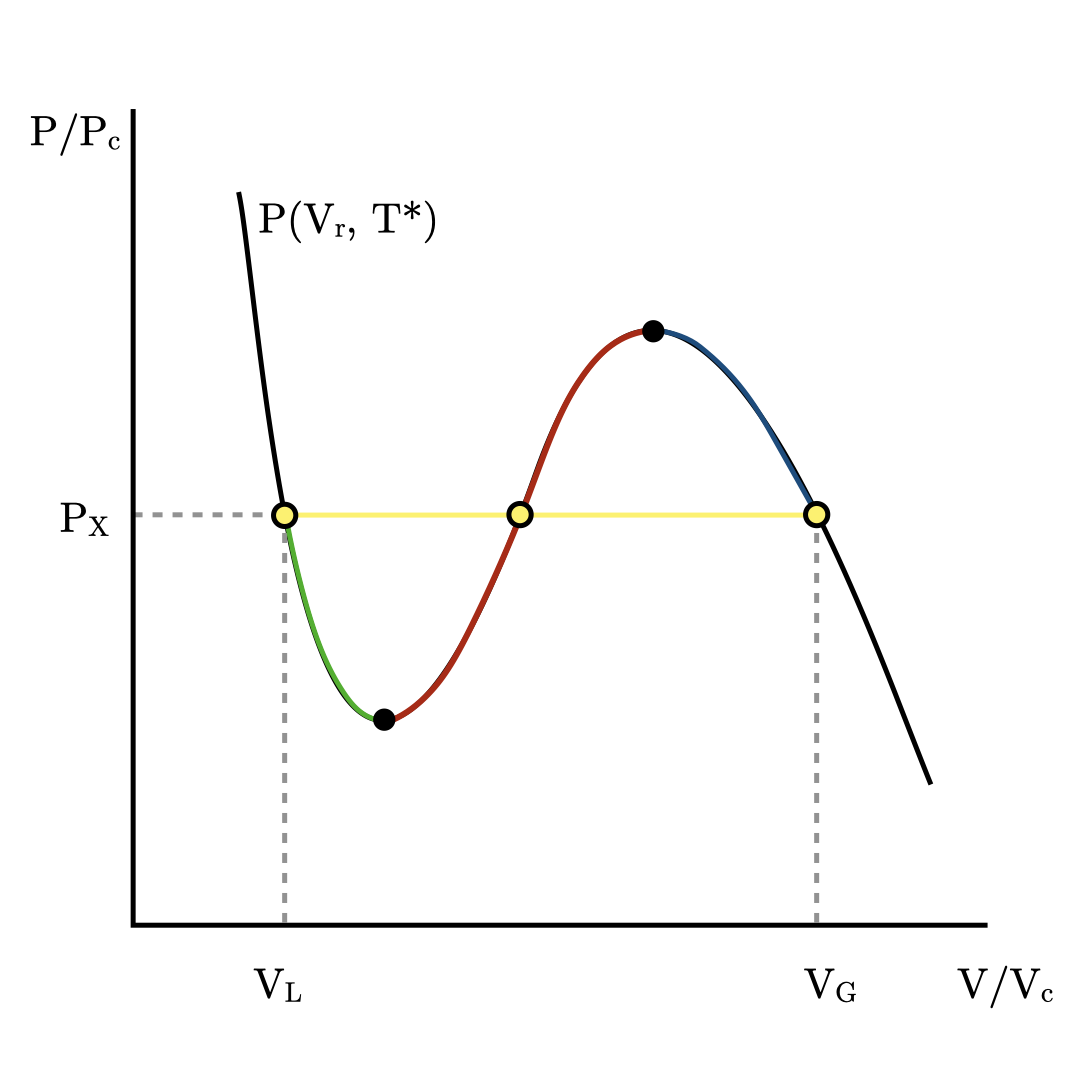
../_images/vdw_isotherm.png — Рис. 6.2 Изотерма ван дер Ваальса при температуре ниже критической.#

Красный участок на изотерме соответствует запрещённым термодинамическим состояниям, поскольку \(\partial P_r / \partial V_r > 0\). Жёлтый участок изобары \(P_X\) соответствует давлению, при котором при данной температуре \(T^*\) жидкая и газовая фазы сосуществуют. При объёмах \(V_r < V_L\) всё вещество находится в жидком состоянии, а при объёмах \(V_r > V_G\) в газовом. Синий и зелёный участки изотермы соответствуют метастабильным состояниям.

Можно вычилисть ряд величин \(V_L\) и \(V_G\) для диапазона температур, тогда получим границу двухфазной области.

../_images/vdw_task_answer.svg — Рис. 6.3 Уравнение ван дер Ваальса. Сплошными линиями показаны изотермы для ряда температур. Красная линия с точками соответствует бинодали: это граница значений давлений и объёмов \(V_L\), \(V_G\), при которых возможно двухфазное состояние. Красная область под бинодалью – двухфазная область.#

Чтобы для данной температуры \(T^*\) определить равновесные объёмы \(V_G\), \(V_L\) и давление \(P_X\), требуется находить минимум потенциала Гельмгольца. Это требует решения нелинейной системы, но можно поступить иначе.

Лекнером [Lek82] предложена параметризация величин для двухфазного равновесия. В качестве параметра используется \(y = \Delta s / 2\), где \(\Delta s\) представляет собой скачок энтропии на частицу между газовой и жидкой фазами в единицах \(k_B\). Для параметризации используются функции \(f(y)\) и \(g(y)\)

\[\begin{split}\begin{align} f(y) &= \frac{y \cosh{y} - \sinh{y}}{\sinh{y}\cosh{y}-y},\\ g(y) &= 1 + 2 f(y) \cosh{y} + f^2(y), \end{align}\end{split}\]

через которые выражаются термодинамические величины.

Так, приведённые температура \(T_X\) и давление \(P_X\) задают \((P, T)\)-границу двухфазного равновесия. Функции параметризованы следующим образом

\[\begin{split}\begin{align} T_X(y) &= \frac{27 f(y)[f(y) + \cosh{y}]}{4g^2(y)},\\ P_X(y) &= \frac{27 f^2(y)[1 - f^2(y)]}{g^2(y)}.\\ \end{align}\end{split}\]

Задание

Ваша задача состоит в том, чтобы определить \(V_L\) и \(V_G\) для ряда температур \(T_r \in [0.85, 1]\) и соответствующих им давлений, получив таким образом границу фазового равновесия. Нанесите полученные точки \((P_X, V_L)\) и \((P_X, V_G)\) поверх изотерм, как на Рисунке 6.3.

Совет

Подробную информацию об уравнении ван дер Ваальса можно получить из статьи [Joh14].