8. Автоматическое дифференцирование#
Автоматическое дифференцирование является способом вычисления производных функции, заданной программно. Этот вид дифференцирования опирается на правило дифференцирования сложной функции, представление функции в виде последовательности элементарных операций и перегрузке программных инструкций (функций, операторов).
Автоматическое дифференцирование не является численным дифференцированием. Численное дифференцирование приближает производную на основе её определения \(f'(x) \approx (f(x) + f(x + \delta x)) / \delta x\). В то время как автоматическое дифференцирование не требует введения шага \(\delta x\), а производная вычисляется точно (в пределах машинной арифметики).
Автоматическое дифференцирование не является символьным дифференцированием. Символьное дифференцирование преобразовывает выражения и применяет правила дифференцирования, чтобы получить выражение производной \(f'(x)\). Впоследствии полученное выражение можно вычислить (и даже создать исходный код для производной). В автоматическом дифференцировании отсутствует программное представление функции в виде математического (символьного) выражения.
Сравнение способов дифференцирования показано на Рисунке 8.1.
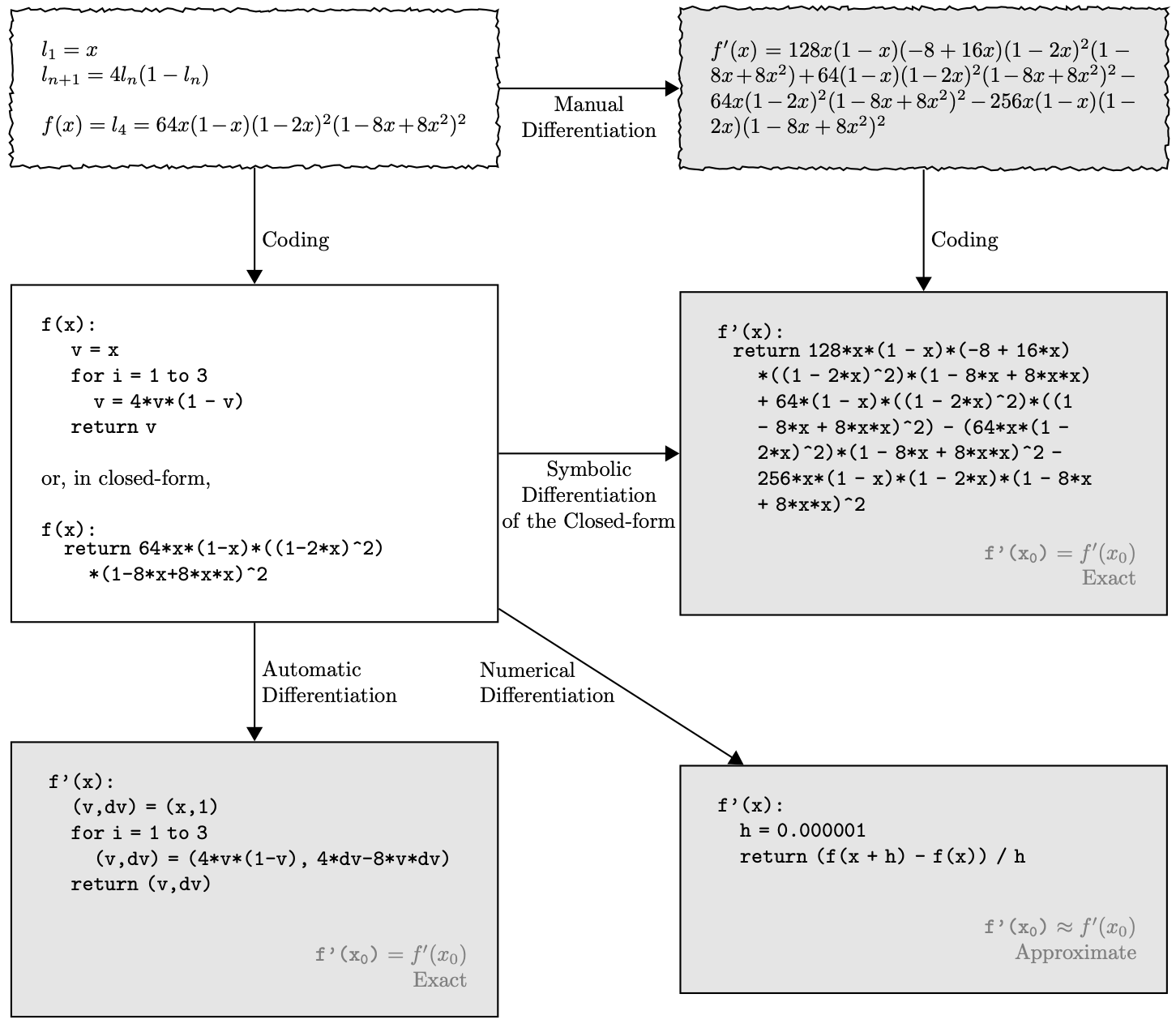
Рис. 8.1 Способы дифференцирования.
Символьное вычисление даёт точный результат, но требует преобразования кода f к closed-form;
численное дифференцирование неточно ввиду погрешностей метода и округления;
автоматическое дифференцирование точно и позволяет использовать управляющие конструкции языка.
Источник: [BPRS18].#
Примечание
С автоматическим дифференцированием связано понятие «дифференцируемого» программирования (differential programming). Это подход к написанию кода, который учитывает возможность автоматически дифференцировать запрограммированные функции.
В данной главе изложены темы дуальных чисел, графа вычислений, а также автоматического дифференцирования вперёд и назад. Чтение главы вы можете начать с Раздела 8.2 (Дуальные числа), пропустив Раздел 8.1 (Метод комплексного шага).
Совет
Подробнее с автоматическим дифференцированием вы можете ознакомиться в следующих работах.
Kochenderfer and Wheeler [KW19].
Дмитрий Кропотов. Автоматическое дифференцирование. ВМК МГУ, кафедра математических методов прогнозирования. https://youtu.be/za2LgI8JFCw.
Baydin, Pearlmutter, Radul, and Siskind [BPRS18].