1.7. Типы, методы и multiple dispatch

В Julia типы упорядочены в дерево, образуя систему. В этом дереве есть самые разные ветви: для числовых типов, строковых, массивов… В свою очередь, для функции можно написать любое количество методов, указывая в объявлении метода при каком наборе типов аргументов, или даже целых ветвей, он будет вызываться. Процесс выбора метода при вызове функции называется диспетчеризацией. Диспетчеризация учитывает типы всех позиционных аргументов, поэтому она называется множественной. При первом вызове функции или метода Julia, если возможно, создаёт для него эффективную (машинную) реализацию.

Эти три инструмента: дерево типов, методы и диспетчеризация, являются ядром дизайна языка Julia, дающим гибкость в написании кода вообще и быстрого кода в частности.

Подробнее о рассматриваемых здесь темах можно почитать в разделах Types, Methods и wiki:Multiple dispatch.

1.7.1. Система типов

В Julia сильная динамическая система типов.

Однако, стоит избегать и потенциально предугадывать места, в которых переменная меняет свой тип. Компилятор вас поощрит.

Поскольку в Julia динамическая типизация, то переменная может менять свой тип в процессе работы программы.

julia> x = 5
5

julia> typeof(x)
Int64

julia> x  = 5.0
5.0

julia> typeof(x)
Float64

В Julia нельзя указать, чтобы переменная имела постоянное значение, но можно указать, что переменная не меняет свой тип

julia> const y = 10
10

julia> y = 10.0
ERROR: invalid redefinition of constant y
Stacktrace:
 [1] top-level scope
   @ REPL[6]:1

julia> y = 20
WARNING: redefinition of constant y. This may fail, cause incorrect answers, or produce other errors.
20

Julia не допустила присвоение y = 10.0, потому что оно меняет тип переменной y::Int64. Однако, присваивать значения Int64 переменной y всё-таки можно, но не стоит этого делать.

1.7.1.1. Декларация типов

С помощью оператора :: вы можете декларировать тип объекта. Обычно это делается для

• переменных;

• аргументов функции;

• возвращаемого функцией значения;

• полей композитных типов (структур).

Конвертацию делает функция convert(T, x). Правила конвертации можно задавать.

Например, вы можете декларировать тип переменной внутри функции (или другой локальной области видимости). В таком случае при присвоении значения происходит конвертация.

julia> function foo()
           x::Int8 = 100
           return x
       end
foo (generic function with 1 method)

julia> x = foo()
100

julia> typeof(x)
Int8

julia> typeof(100)
Int64

Также вы можете декларировать тип возвращаемого значения функцией (хотя, делается это редко, поскольку компилятор выводит типы, если возможно).

julia> bar()::Int8 = 100
bar (generic function with 1 method)

julia> bar()
100

julia> typeof(bar())
Int8

1.7.1.2. Какие бывают типы

Типы в Julia классифицируются по следующим признакам (указаны не все)

• абстрактный abstract (AbstractFloat) и конкретный concrete (Float64);

• примитивный primitive (Float64) и композитный composite (Complex{Float64});

• параметрический parametric (Complex{Float64});

• изменяемый (Vector{Float64}) и неизменяемый (Tuple{Float64,Float64});

• …

В Julia система типов организована в дерево, корень которого тип Any, т.е. любой. Листьями дерева типов являются конкретные типы. У значения такого типа известна структура в памяти. Абстрактные типы нужны в качестве промежуточных узлов дерева типов, выстраивая иерархию.

Примечание

Кроме того, объявление неабстрактного параметрического типа T1{T2} создаёт UnionAll тип T1. Последний ведёт себя как супертип (родительский) для параметризованных потомков.

Например, Rational{T} порождает UnionAll Rational, и Rational будет супертипом для всех Rational{T}: Rational{Int64}, Rational{Int8}…

В дереве ниже UnionAll типы помещены в параллелограммы.

Например, так выглядит часть дерева с числовыми и строчными типами, при этом

• конкретные типы указаны в округлённых рамках;

• абстрактные в прямоугольных.

flowchart TB Any --> Number --> Real --> Integer Any --> AbstractString --> String([String]) AbstractString --> SubString[/SubString/] Number --> Complex[/Complex/] Real --> AbstractFloat Real --> Rational[/Rational/] Rational --> RationalInt64(["Rational{Int64}"]) Rational --> RationalInt32(["Rational{Int32}"]) Integer --> Int64([Int64]) Integer --> Int32([Int32]) Integer --> Int16([Int16]) Integer --> Int8([Int8])

Несколько функций для интроспекции системы типов

• subtypes(T): подтипы типа T;

• isabstracttype(T): является ли тип T абстрактным;

• isprimitivetype(T): является ли тип T примитивным;

• ismutable(x): является ли значение x изменяемым.

С точки зрения дерева, можно ли из Ty добраться до Tx.

Также с помощью subtype-оператора Tx <: Ty можно проверять «является ли тип Tx подтипом типа Ty».

julia> Int64 <: Number
true

Примитивные типы представляются в виде набора бит. Примерами являются Int-ы и Float-ы.

Примечание

Создание собственных абстрактных и примитивных типов здесь не разбирается.

1.7.1.3. Композитные типы

Композитный тип имеет более сложную структуру в памяти, чем примитивный тип. Этот тип является набором именованных полей, а экземпляром такого типа можно манипулирвовать как одним значением. В других языках им соответствуют объекты (objects) или структуры (structs). Примерами встроенных композитых типов являются Complex{T}, Rational{T}, Tuple, String, Array, IO…

Ниже показан пример композитного типа для точки на плоскости.

julia> struct Point
           x        # то же, что и x::Any, т.е. поле может быть либого типа
           y::Int   # так указывается тип (можно и абстрактный)
       end

julia> p1 = Point(1.0, 2)
Point(1.0, 2)

julia> typeof(p1)
Point

julia> p1.x
1.0

julia> p1.x = 9
ERROR: setfield! immutable struct of type Point cannot be changed
...

По умолчанию, структуры в Julia неизменяемые. Перезапись поля можно разрешить, сделав структуру изменяемой (mutable).

julia> mutable struct MPoint
           x
           y
       end

julia> mp1 = MPoint(1, 2)
MPoint(1, 2)

julia> mp1.x = 10
10

julia> mp1
MPoint(10, 2)

Иногда это может приводить к замедлению работы, поскольку mutable struct (или её часть) выделяется в куче, а не на стеке.

Тем не менее, в поле обычной структуры можно хранить значение изменяемого типа. В таком случае поле хранит ссылку на изменяемый объект. Объект поменять можно, а ссылку – нет. Например, так хранятся массивы внутри структур.

Конструктор (constructor) Point(x, y) для композитного типа можно поменять или создать несколько. Конструкторы бывают внутренние (inner constructor) и внешние (outer constructor). Внутренние конструкторы объявляются внутри объявления структуры, и в этом случае конструктор по умолчанию теряется. Внешние конструкторы, по сути, функции для удобного создания экземпляров структур. Обычно такие функции имеют то же имя, что и тип. Такое возможно благодаря механизму методов, о котором говорится далее.

1.7.1.4. Параметрические композитные типы

Абстрактные параметрические типы тоже существуют.

Параметрический тип это тип, который в своём объявлении содержит дополнительную информацию. Например, тип Complex в языке объявлен следующим образом [source].

struct Complex{T<:Real} <: Number
    re::T
    im::T
end

С практической точки зрения, код выше объявляет структуру данных Complex для комплексных чисел, которые (сюрприз) являются числами (Number). Т.е., подразумевается, что с ними можно совершать все арифметические операции. Сама структура данных состоит из двух действительных (Real) чисел с одинаковым типом.

Более строго, объявление выше значит

Complex в данном случае ни абстрактный, ни конкретный.

• создать UnionAll-тип Complex, который будет вести себя как супертип для Complex{T};

• создать параметрический тип Complex{T},

• где параметр T является подтипом типа Real,

• при этом типы Complex и Complex{T} являются подтипами Number;

• у Complex{T} два поля: re и im, каждое из них имеет тип T.

Это не значит, что массив в Julia может хранить только значения одного типа. Ведь есть абстрактные типы: Any, Number…

В качестве параметров могут быть типы и значения примитивных типов. Например, в Julia объявлен тип для массивов AbstractArray{T,N}, где под T подразумевается тип значений, а под N размерность массива (1 для векторов, 2 для матриц…).

Параметрические типы порождают целое семейство типов. Член такого семейства – любая комбинация разрешенных значений параметров типа.

Таким образом, с помощью параметризации композитного типа мы можем дать подсказки для компилятора, чтобы тот создавал оптимизированный код.

1.7.1.4.1. Пример

Рассмотрим две версии Point

julia> struct APoint
           x
           y
       end

julia> struct TPoint{T}
           x::T
           y::T
       end

Создадим функцию, вычисляющую расстояние от точки до начала координат

julia> dist(p) = sqrt(p.x^2 + p.y^2)
dist (generic function with 1 method)

Заметьте, в этой функции нет никаких ограничений на тип аргумента p.

Создадим два массива случайных точек

julia> AA = [APoint(rand(2)...) for _ in 1:1_000_000];

julia> TA = [TPoint(rand(2)...) for _ in 1:1_000_000];

julia> typeof(AA), typeof(TA)
(Vector{APoint}, Vector{TPoint{Float64}})

Про массив TA компилятор явно знает больше, судя по typeof.

Измерим время работы. Точный бенчмарк показывает разницу времени работы в два порядка.

julia> using BenchmarkTools

julia> @btime dist.(AA);
  117.766 ms (4999502 allocations: 83.92 MiB)

julia> @btime dist.(TA);
  1.290 ms (5 allocations: 7.63 MiB)

Почему? Дело в том, что тип APoint не параметризован, и с точки зрения компилятора в его полях может находится всё что угодно (Any). Поэтому, всякий раз совершая операцию над полем такой структуры, необходимо проверять, что в этом поле содержится и можно ли операцию совершать вообще. Тип TPoint, напротив, параметризован. Создав такой объект, компилятору известны типы его полей, а значит и полное представление объекта в памяти. Поэтому можно создать эффективный код для функции dist при вызове от TPoint{Float64}, ведь известно, что p.x и p.y это Float64 числа, а для них определены операции возведения в степень, сложение и извлечение корня. А вызывая dist от TPoint{Float64} в дальнейшем, можно сразу пользоваться скомпилированной версией.

Совет

Поисследовать, может ли компилятор предугадать типы в теле вызова можно с помощью макроса @code_warntype

julia> @code_warntype dist(APoint(1, 2))
Variables
  #self#::Core.Const(dist)
  p::APoint

Body::Any
1 ─ %1  = Base.getproperty(p, :x)::Any
│   %2  = Core.apply_type(Base.Val, 2)::Core.Const(Val{2})
│   %3  = (%2)()::Core.Const(Val{2}())
│   %4  = Base.literal_pow(Main.:^, %1, %3)::Any
│   %5  = Base.getproperty(p, :y)::Any
│   %6  = Core.apply_type(Base.Val, 2)::Core.Const(Val{2})
│   %7  = (%6)()::Core.Const(Val{2}())
│   %8  = Base.literal_pow(Main.:^, %5, %7)::Any
│   %9  = (%4 + %8)::Any
│   %10 = Main.sqrt(%9)::Any
└──       return %10

julia> @code_warntype dist(TPoint(1, 2))
Variables
  #self#::Core.Const(dist)
  p::TPoint{Int64}

Body::Float64
1 ─ %1  = Base.getproperty(p, :x)::Int64
│   %2  = Core.apply_type(Base.Val, 2)::Core.Const(Val{2})
│   %3  = (%2)()::Core.Const(Val{2}())
│   %4  = Base.literal_pow(Main.:^, %1, %3)::Int64
│   %5  = Base.getproperty(p, :y)::Int64
│   %6  = Core.apply_type(Base.Val, 2)::Core.Const(Val{2})
│   %7  = (%6)()::Core.Const(Val{2}())
│   %8  = Base.literal_pow(Main.:^, %5, %7)::Int64
│   %9  = (%4 + %8)::Int64
│   %10 = Main.sqrt(%9)::Float64
└──       return %10

1.7.2. Методы и multiple dispatch

Для каждой функции в Julia можно определить сколько угодно методов (methods). Это способ полиформизма в языке. Вы уже с ним сталкивались, например, 1 + 2 и 1.0 + 2.0 совершенно разные вызовы. В первом случае вызывается метод +(x, y) для Int64, а во втором метод +(x, y) для сложения Float64.

Вообще, у сложения + в базовой библиотеке Julia 1.6.2 190 методов. Здесь методы и для примитивных типов, для комплексных и рациональных чисел, для векторов, матриц, тензоров…

julia> methods(+)
# 190 methods for generic function "+":
[1] +(x::T, y::T) where T<:Union{Int128, Int16, Int32, Int64, Int8, UInt128, UInt16, UInt32, UInt64, UInt8} in Base at int.jl:87
[2] +(c::Union{UInt16, UInt32, UInt64, UInt8}, x::BigInt) in Base.GMP at gmp.jl:528
[3] +(c::Union{Int16, Int32, Int64, Int8}, x::BigInt) in Base.GMP at gmp.jl:534
...

Узнать, какой метод вызвался можно макросом @which.

julia> @which 1 + 2
+(x::T, y::T) where T<:Union{Int128, Int16, Int32, Int64, Int8, UInt128, UInt16, UInt32, UInt64, UInt8} in Base at int.jl:87

julia> @which 1.0 + 2.0
+(x::Float64, y::Float64) in Base at float.jl:326

julia> @which 1.0 + 2
+(x::Number, y::Number) in Base at promotion.jl:321

Можно сказать, что функция определяет дефолтное действие с аргументами. А методы функции содержат частные реализации этих действий на случаи тех или иных аргументов. Например, метод sum для вектора сложит все элементы и это займёт линейное время, а sum для арифметической прогрессии займёт константное время, используя формулу. При этом с точки зрения пользователя сигнатура вызова одна и та же: sum(A).

Процесс выбора нужного метода называется диспетчеризацией (dispatch). В Julia диспетчеризация производится по типам всех позиционных аргументов функции. Этот механизм называется multiple dispatch. Он гибче и продуктивнее, нежели диспетчеризация по одному типу, например, как в Python (type(x).__add__(x, y)). При этом, в отличие от языков со статической типизацией, нет необходимости указывать типы аргументов.

Строго говоря, generic function единственна, а методов у неё много. Однако, всё же принято называть методы функциями, если контекст позволяет.

Методы создаются как функции, но с указанием типа хотя бы одного аргумента.

julia> f(x, y) = 2x + y
f (generic function with 1 method)

julia> f(x::Float64, y::Float64) = 3x + y
f (generic function with 2 methods)

julia> methods(f)
# 2 methods for generic function "f":
[1] f(x::Float64, y::Float64) in Main at REPL[28]:1
[2] f(x, y) in Main at REPL[26]:1

Здесь же посмотрим на диспетчеризацию

julia> f(1, 1)
3

julia> f(1.0, 1.0)  # два Float64, подходит f(x::Float64, y::Float64)
4.0

julia> f(1.0, 1)    # Float64 и Int64, подходит f(x, y)
3.0

Конечно, использование не конкретных типов разрешено

julia> f(x::Complex, y::Complex) = 5x + y*im
f (generic function with 3 methods)

julia> f(1.5im, 2.5im)
-2.5 + 7.5im

julia> f(1.5im, 2.5)
2.5 + 3.0im

При диспетчеризации может возникать коллизия: два или более метода подходят для вызова. В этом случае Julia выдаст ошибку MethodError.

Совет

Визуализацию диспетчеризации в Julia можно посмотреть в этой статье из блога Matthijs Cox.

1.7.3. Стабильность по типу

Когда Julia исполняет функцию (или метод) в первый раз, компилятор «на лету» создаёт машинный код и запоминает его для последующих вызовов уже без компиляции. Получившийся код лишь может быть по-настоящему машинно-эффективным (как в компилирующихся языках, например, в C/C++ или Fortran). Например, если в вашей функции содержится переменная, тип которой можно узнать только при исполнении (runtime), то эффективной реализации исходного кода, касающегося работы с этой переменной, не получится. В этом случае какую-либо операцию с такой переменной необходимо проверять: существует ли она и, если существует, то где определена. С другой стороны, если по типам аргументов при вызове функции компилятору понятно, какие типы у всех остальных переменных, включая возвращаемое значение, то созданный машинный код будет эффективным.

В итоге, программы на Julia могут быть быстрыми, как в компилируемых языках, но могут быть и медленными, как в интерпретируемых языках. Чтобы писать быстродействующие программы, стоит разбивать исходный код на небольшие функции, а в каждой из них поддерживать стабильность типов.

Определение 1.2 (Стабильная по типу функция)

Функция, тип возвращаемого значения которой зависит только от типов аргументов, и не зависит от их значений, называют стабильной по типу (type stable function).

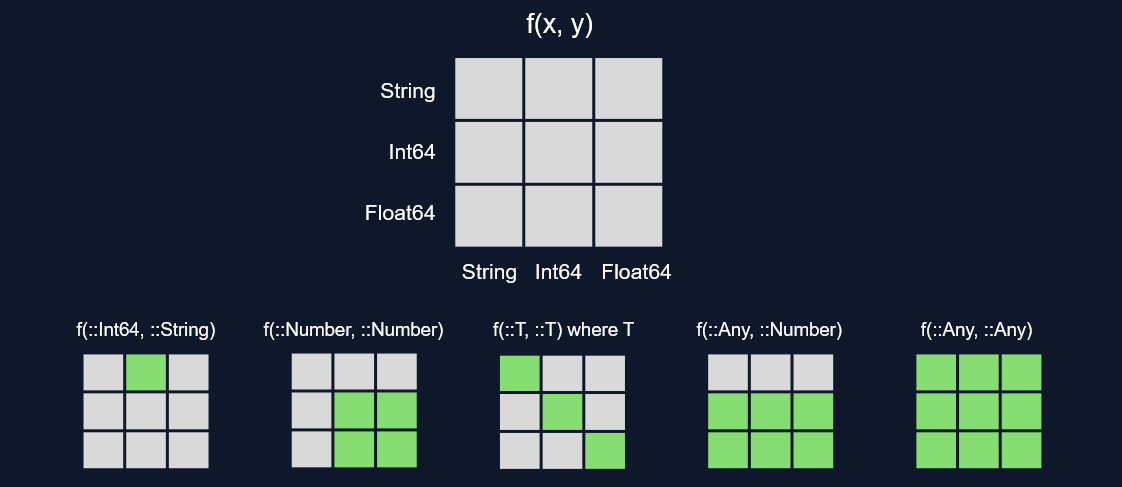
Рассмотрим для примера функцию f(x, y) = x^2 + y^2. При первом вызове от двух Int (например, f(3, 4)) компилятор удачно выводит типы всех значений внутри функции: x^2 == 9 и y^2 == 16 это два Int, а их сумма 25 (возвращаемое значение) также Int. Более того, при любых вызовах вида f(::Int, ::Int) промежуточные значения и возвращаемое значение будут типа Int. Поэтому можно создать машинную реализацию для вызова f(::Int, ::Int) и использовать её в дальнейшем. Аналогично компилятор поступит для вызовов вида f(::Float64, ::Int), f(::Int, ::Float64) и f(::Float64, ::Float64).

Таблица 1.4 Типы промежуточных значений для функции f(x, y) = x^2 + y^2.

	f(::Int, ::Int)	f(::Float64, ::Int)	f(::Float64, ::Float64)
x^2	Int	Float64	Float64
y^2	Int	Int	Float64
x^2 + y^2 (return)	Int	Float64	Float64

В нашем примере стабильные по типу функции это ^(x, y), +(x, y) и сама f. При этом стабильность по типу функции f в нашем случае обеспечивается стабильностью функций + и ^. Для таких функций компилятору известно устройство в памяти входных и выходных значений, что позволяет создавать эффективный код.

Покажем также пример нестабильной по типу функции.

g(x::Real) = x > 0 ? x : 0

В этом случае при вызове g(::Int) функция стабильна по типу, поскольку для любых x::Int возвращется Int. Однако, вызов вида g(::Float64) не стабилен по типу, поскольку для положительных x::Float64 возвращается число типа Float64, а для отрицательных — число типа Int. Добиться стабильности для вызова g(::Float64) можно было бы добавлением метода g(x::Float64) = x > 0 ? x : 0.0, но тогда подобные методы требовались бы для всех типов действительных чисел T <: Real. Лучшим вариантом является использование функции-утилиты zero(x): она возращает ноль того же типа, что и x.

g(x::Real) = x > 0 : x : zero(x)

Также рекомендуется заменить x > 0 на x > zero(x), но компилятор, вероятно, сгенерирует идентичный машинный код (проверьте с помощью @code_native).

Показательным примером дизайна стабильной по типу функции в Julia является дизайн функции квадратного корня sqrt(x). Если извлекать квадратный корень из натуральных чисел, то только для некоторых из них (полных квадратов) получим натуральное число, а в остальных случаях получим не целые числа. Разработчики Julia учли эту особенность, и, ради сохранения стабильности, вызов sqrt(::Int) всегда возвращает Float64, даже для полных квадратов. Кроме того, если извлекать корень из отрицательного числа, то получим число комплексное. Поэтому sqrt(x::Real) требует неотрицательного числа, чтобы независимо от значения x возвращать Float64. А для извлечения корней из отрицательных чисел требуется использовать метод вида sqrt(x::Complex) (например, sqrt(-1 + 0im) вместо sqrt(-1)). В последнем случае всегда возвращается Complex число, что сохраняет стабильность по типу функции sqrt.

Для создания стабильных по типу функций Julia предоставляет множество инструментов. Например,

• zero(x) и one(x) для создания нуля и единицы того же типа, что и x,

• similar(x) для создания массива того же типа и размера, что и x,

• iszero(x) и isone(x) вместо x == 0 и x == 1,

• isodd(x) и iseven(x) вместо x % 2 == 1 и x % 2 == 0,

• isnan(x) и isinf(x) для проверки на Not-a-Number и бесконечность.

Часто используется функция promote(x...), которая подбирает «общий» тип для своих аргументов и приводит их к нему.

julia> promote(1, 2.0, 3//4)
(1.0, 2.0, 0.75)

А для проверки своего кода на стабильность по типу можно использовать макрос @code_warntype.

1.7.4. Интерфейсы

На методах основаны интерфейсы в языке. Например, для типа точки на декартовой плоскости, рассмотренном выше, вы можете определить оператор сложения. Вы также можете создать вектора из точек. Сложение таких векторов определять уже не нужно: операция сложения для векторов происходит поэлементно и определено в стандартной библиотеке. Поэтому, определив арифметические операции для точки, вам автоматически доступны методы линейной алгебры (LinearAlgebra) и, например, статистики (Statistics).

Вы можете создавать собственные структуры данных, у которых будет поведение коллекций. Как только вы объявите необходимые методы интерфейса для своего типа, вы сможете пользоваться всеми функциями, определенными для коллекций. Или, скажем, вы можете встроить свои структуры данных в интерфейс цикла for.

С помощью методов также создаются типы, ведущие себя как функции: их можно вызывать (callable). На этом основаны замыкания (closures) в Julia.

Один из ярких примеров это автоматическое дифференцирование вперёд. Можно определить дуальное число и математические операции с ним. Затем подать это число на вход любой функции от числа. При вызове такой функции от действительного числа возвращается её значение. А при вызове от дуального числа возвращается значение функции и её производной. То есть, программисту не нужно аналитически вычислять производную и переносить её в код отдельной функцией: можно воспользоваться дуальным числом.

Изобретено множество дизайн-паттернов с использованием методов и типов. За подробностями по теме методов обращайтесь в мануал [url]. Много паттернов описано в книге [Kwo20].